Skip to content

Part 1 - Solutions

Solutions

Exercise 1: optimize the mass window: expected/observed significance {#exercise-1-optimize-the-mass-window-expectedobserved-significance .unnumbered}

  1. Use function Significance_Optimization(1.00).\ For Lumi scale factor = 1.00\ Expected: optimal window = 7.15 GeV \(\rightarrow\) expected significance = 2.04 sigma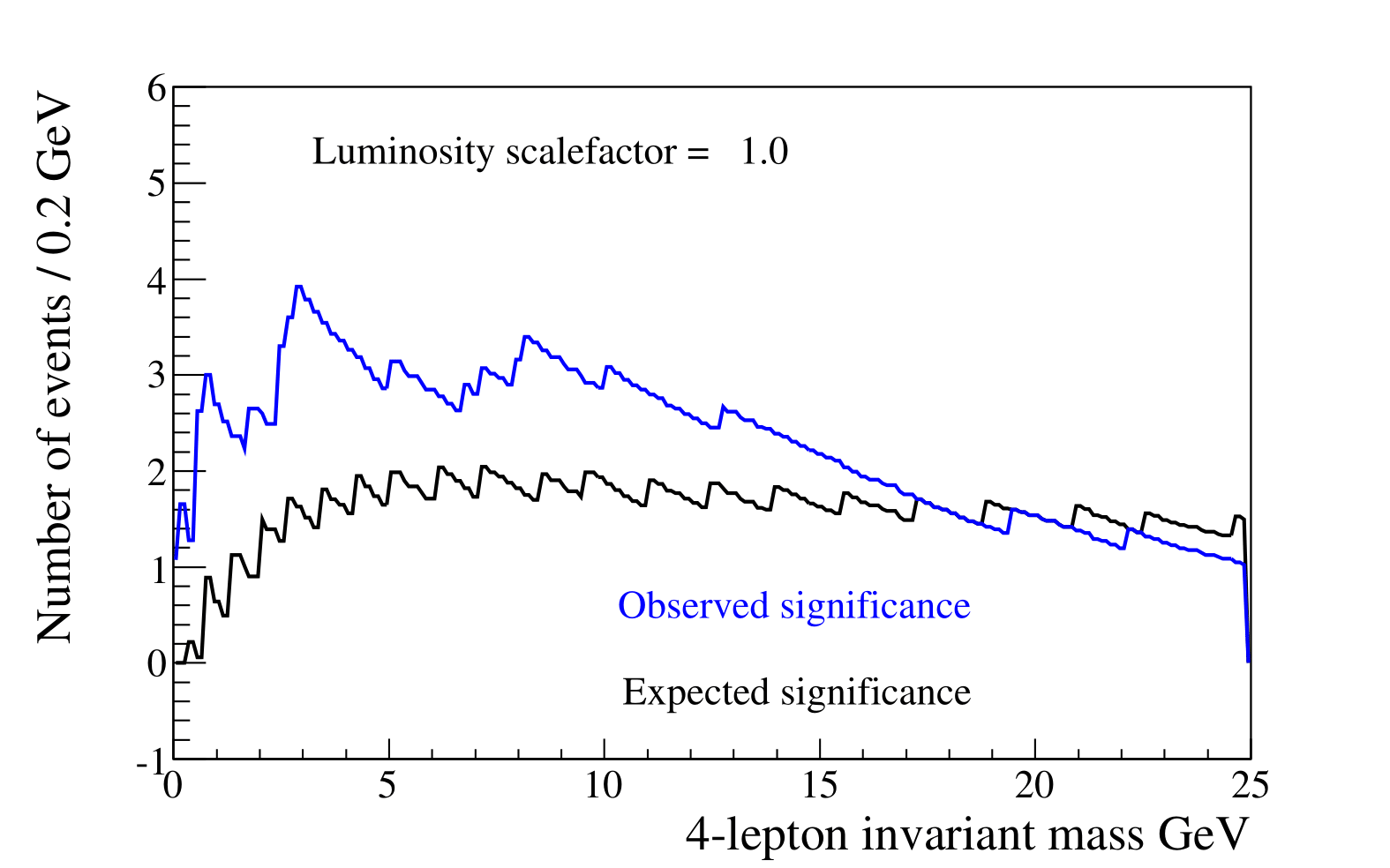 Figure 1: Significance versus width mass window around 125 GeV

    Funny 'peaked' shape is related to the rounding to integer number of events needed to integrate the Poisson distribution when computing the p-value.

  2. Use function Significance_Optimization(1.00): Lumi scale factor = 1.00\ Observed: optimal window = 2.85 GeV \(\rightarrow\) observed significance = 3.92 sigma

  3. Use function Significance_Optimization(5.00): Lumi scale factor = 5.00\ Expected: optimal window = 6.55 GeV \(\rightarrow\) expected significance = 4.79 sigma

  4. Use function Significance_Optimization(x) and vary x. Expected significance above 5 sigma for first time at Lumi scale factor of 5.40.\ For Lumi scale factor = 5.40\ Expected: optimal window = 6.35 GeV \(\rightarrow\) expected significance = 5.02 sigma