Part 3 - Solutions
Solutions
Exercise 4: compute the test statistic
-
See function
Get_TestStatistic(). -
Use
Significance_LikelihoodRatio_ToyMCValue of the test-statistic for the 'real' data-set: X = -11.53.Note that this routine is designed for the next part of the exersise, but you can see how it is done.
Exercise 5: create toy data-sets
-
Look at function
GenerateToyDataSet(TH1D *h_mass_template). -
Look for the implementation as part of exercise a).
-
For 10,000 toy experiments you get the distribution by running
Significance_LikelihoodRatio_ToyMC(10000,2), where the \(2^{\rm nd}\) option gets you the coloured one and two sigma error regions on the b-only distribution.
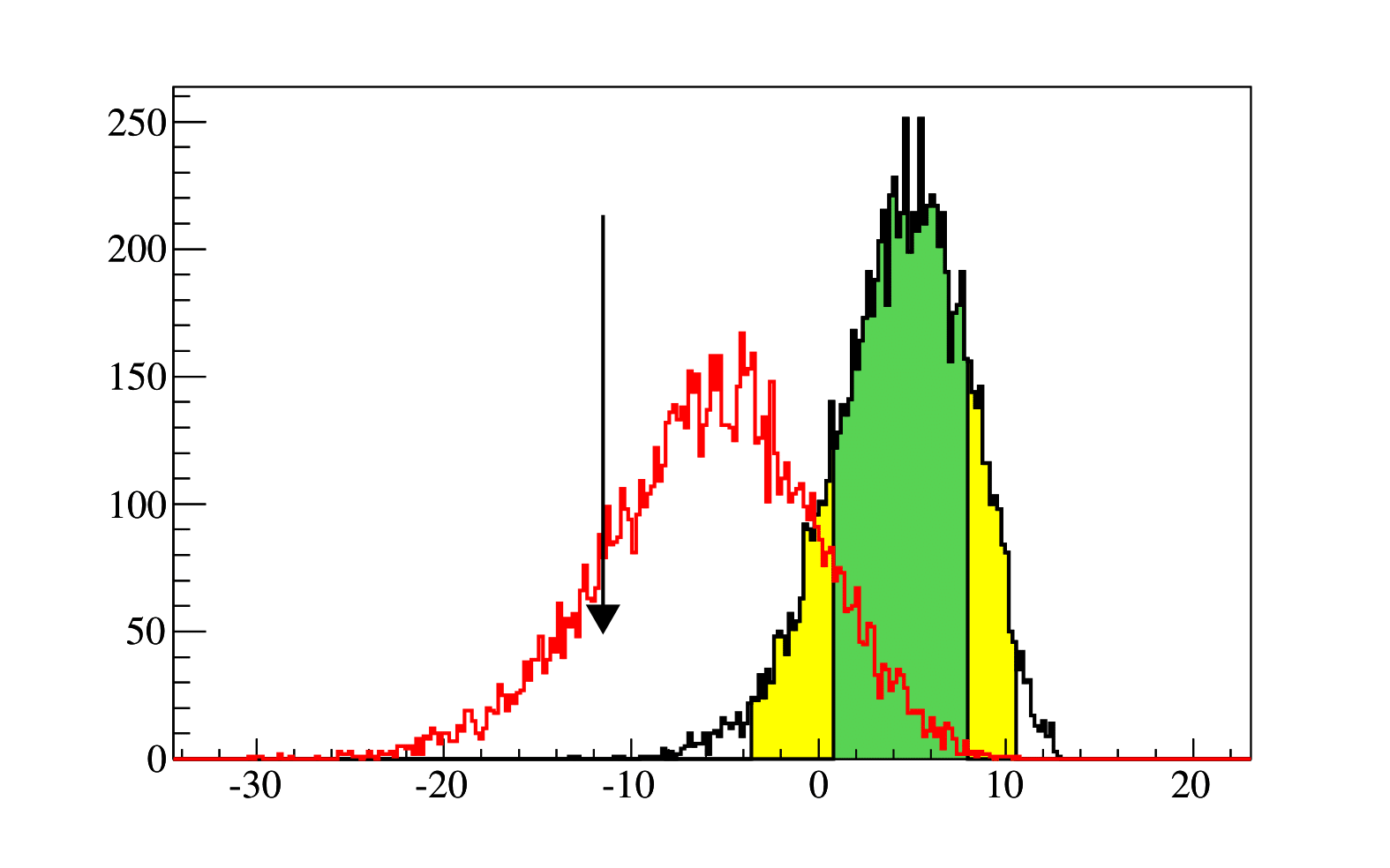
The value of the test-statistic \(X\) are for:
- median s+b experiment: X = -5.7
- median b-only experiment: X = 4.7
- data: X = -11.53
As we see, the excess in the data is even larger than we expect if a Higgs boson would be present.
Exercise 6: Discovery-aimed: compute p-values
-
Compute the p-value or \({\rm 1-CL_b}\) (under the b-only hypothesis): For 10,000 toy experiments you get the distribution by running
Significance_LikelihoodRatio_ToyMC(10000,2), where the second option gets you the coloured one and two sigma error regions on the b-only distribution.The values for \({\rm 1-Cl_{b}}\) are for:
-
median s+b experiment: \({\rm 1-CL_{b}}\) = 6.70e-03 (2.47 sigma)\
- median b-only experiment: \({\rm 1-CL_{b}}\) = 0.500 (0.00 sigma)\
-
data: \({\rm 1-CL_{b}}\) =2.00e-04 (3.54 sigma)
-
Draw conclusions:
The observed significance is 3.54 sigma. This is smaller than 5 sigma so we can not claim a discovery. The expected significance is 2.47 sigma. This is smaller than 5 sigma so we did not expect to be able to make a discovery. To see how the expected significance increases you can try to redo this study, but scaling the luminosity. In the answers we only included a scale factor for the signal. Introduce a factor that scales the signal and background yield and see at what luminosity scale-factor the expected significance exceeds 5 sigma. Note that you do not have time to run tens of millions of toys. Take a few points and try to extrapolate.
Exercise 7: Exclusion-aimed: compute \({\rm CL_{s+b}}\)
-
Compute the \({\rm CL_{s+b}}\) (under the s+b-only hypothesis):
The values for \({\rm Cl_{s+b}}\) are for:
-
median s+b experiment: \({\rm CL_{s+b}}\) = 0.5000\
- median b-only experiment: \({\rm CL_{s+b}}\) = 0.0227\
-
data: \({\rm CL_{s+b}}\) = 0.8425
-
Draw conclusions:
The expected \(Cl_{s+b}\) for the average b-only experiment is 0.0227. As this is smaller that 0.05, we expected to be able to exclude the \({\rm m_h}\)=125 GeV hypothesis. However, as the (observed) value of \(Cl_{s+b}\) in the data is 0.84, we cannot exclude this hypothesis. This is not so weird, since we see an excess of events. Even more, we even more events than we expected in the case the Higgs boson would be present in the data. We can now increase the signal cross-section scale factor using the third parameters in the function
Significance_LikelihoodRatio_ToyMC()to see what value of the signal cross section we can actually exclude with this data-set. For a signal scale factor of 2.50 for example we would runSignificance_LikelihoodRatio_ToyMC(10000,2,2.50). Scanning the signal scale factor we see: -
scale factor = 2.50: \({\rm Cl_{s+b}}\) in data = 0.0920 (\(
>5\%\) no exclusion) - scale factor = 2.75: \({\rm Cl_{s+b}}\) in data = 0.0477 (\(
<5\%\) excluded)
A more delicate scan (or interpolation from a few points) will find you the signal scale factor you can exclude.